Diffusion
From Wikipedia, the free encyclopedia
| This article may require cleanup to meet Wikipedia's quality standards. Please improve this article if you can. |
| This article needs additional references or sources for verification. Please help improve this article by adding reliable references. (help, get involved!) Unverifiable material may be challenged and removed. |
- This article is about the physical mechanism of diffusion. For alternative meanings, see diffusion (disambiguation).
Diffusion is the movement of particles of a substance from an area of high concentration to an area of low concentration, resulting in the uniform distribution of the substance. For example, diffusion of particles causes a net movement of particles from areas of higher concentration to areas of lower concentration until equilibrium is reached. This is simply the statistical outcome of random motion: diffusion is a spontaneous process (more familiarly known as a "passive" form of transport, rather than "active"). Diffusion can affect a variety of different quantities. Examples include diffusion of concentration, heat, or momentum. Diffusion increases entropy, decreasing Gibbs free energy, and therefore is thermodynamically favorable. Diffusion operates within the boundaries of the Second Law of Thermodynamics because it demonstrates nature's tendency to wind down, as evidenced by increasing entropy.[1]
Diffusion can be described mathematically by the diffusion equation. This equation is derived from Fick's law, which states that the net movement of diffusing substance per unit area of section (the flux) is proportional to the concentration gradient (how steeply the concentration changes in space), and is toward lower concentration. (Thus if the concentration is uniform there will be no net motion.) The constant of proportionality is the diffusion coefficient, which depends on the diffusing species and the material through which diffusion occurs. Fick's law is an assumption that may not hold for a given diffusive system (e.g., the diffusion may depend on concentration in addition to concentration gradient), in which case the motion would not be described by the normal (simple, Fickian) diffusion equation. An analogous statement of Fick's law, for heat instead of concentration, is Fourier's law.
Diffusion can also be described using discrete quantities (the diffusion equation has derivatives and thus applies to continuous quantities). A common model of discrete diffusion is the random walk. A random walk model is connected to the diffusion equation by considering an infinite number of random walkers starting from a non-uniform configuration, where the evolution of the concentration is described by the diffusion equation.
The spreading of any quantity that can be described by the diffusion equation or a random walk model (e.g. momentum, ideas, price) can be called diffusion.
Diffusion is often important in systems experiencing an applied force. In a conducting material, the net motion of electrons in an electrical field quickly reaches a terminal velocity (resulting in a steady current described by Ohm's law) because of the thermal (diffusive) motions of atoms. The Einstein relation relates the diffusion coefficient to the mobility of particles.
In cell biology, diffusion is a main form of transport within cells and across cell membranes.
Contents
|
[edit] Types of diffusion
Diffusion is the movement of particles from an area where their concentration is high to an area that always has low concentration.
Diffusion includes not only diffusion of particles, but transport phenomena occurring within thermodynamic systems under the influence of thermal fluctuations (i.e. under the influence of disorder; this excludes transport through a hydrodynamic flow, which is a macroscopic, ordered phenomenon), basically making both sides of the lipid bilayer of the same saturation of chemicals.
Diffusion is the process through which velocity thermodynamic system at local thermodynamic equilibrium returns to global thermodynamic equilibriums, through the homogenization of the values of its intensive parameters.
- Atomic diffusion
- Light diffusion
- Brownian motion, for example of a single particle in a solvent
- Collective diffusion, the diffusion of a large number of (possibly interacting) particles
- Effusion of a gas through small holes.
- Electron diffusion, resulting in electric current
- Heat flow
- Thermal diffusion
- Itō diffusion
- Knudsen diffusion
- Momentum diffusion, ex. the diffusion of the hydrodynamic velocity field
- Osmosis
- Photon diffusion
- Reverse diffusion
- Self-diffusion
[edit] Diffusion displacement
The diffusion displacement can be described by the following formula
where 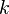 is the dimensions of the system and can be one, two or three.
is the dimensions of the system and can be one, two or three.  is the diffusion coefficient of the particles and
is the diffusion coefficient of the particles and  is time. For the three-dimensional systems the above equation will be:
is time. For the three-dimensional systems the above equation will be:
[edit] Isotope separation
- Gaseous diffusion
- Liquid thermal diffusion
[edit] Diffusion across biological membranes
- Facilitated diffusion
- Ion diffusion through ion channels
- Simple diffusion, not requiring a special protein channel
- Diffusion in the respiratory system - in the alveoli of mammalian lungs, due to differences in partial pressures across the alveolar-capillary membrane, oxygen diffuses into the blood and carbon dioxide diffuses out
such as dye in water it diffuses out to change the colour of water in a matter of seconds. An Experiment to Demonstrate Diffusion Requirements:
1 wide glass tube 2 Corks Cotton wool soaked in ammonia solution 4 square sized red litmus paper
Procedure: Cork the two ends of the wide glass tube. Plug the wet cotton wool with one of the corks and hang the litmus papers with a thread within the tube.
Observation: The red litmus papers turn blue.
Interpretation: The ammonia molecules by diffusion travels from higher concentration which is the cotton wool to lower concentration which is the rest of the glass tube.As the ammonia solution is alkaline, the red litmus papers turn blue. By changing the concentration of ammonia , the rate of color change of the litmus papers can be changed.


