Electrical dipole moment

From Wikipedia, the free encyclopedia

(Redirected from Electric dipole moment)

Jump to: navigation, search

Electrostatics

Electromagnetism
Electricity · Magnetism
Electric charge
Coulomb's law
Electric field
Gauss's law
Electric potential
Electric dipole moment
Magnetostatics
Ampère's circuital law
Magnetic field
Magnetic flux
Biot-Savart law
Magnetic dipole moment
Electrodynamics
Electrical current
Lorentz force law
Electromotive force
(EM) Electromagnetic induction
Faraday-Lenz law
Displacement current
Maxwell's equations
(EMF) Electromagnetic field
(EM) Electromagnetic radiation
Electrical Network
Electrical conduction
Electrical resistance
Capacitance
Inductance
Impedance
Resonant cavities
Waveguides
Tensors in Relativity
Electromagnetic tensor
Electromagnetic stress-energy tensor
This box: view • talk • edit

In physics, the electric dipole moment (or electric dipole for short) is a measure of the polarity of a system of electric charges.

In the simple case of two point charges, one with charge $+ q$ and one with charge $- q$ , the electric dipole moment is:

$\mathbf{p} = q \, \mathbf{r}$

where r is the displacement vector pointing from the negative charge to the positive charge. This implies that the electric dipole moment vector $\mathbf{p}$ points from the negative charge to the positive charge. Note that the electric field lines run in the opposite direction, i.e. away from the positive charge and toward the negative charge. There is no inconsistency here, because the electric dipole moment has to do with the positions of the charges, not the field lines.

More generally, for a system with an arbitrary number of point charges, the electric dipole moment is

$\mathbf{p} = \sum_{i=1}^N \, q_i \, \mathbf{r}_i$

where each 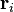$\mathbf{r}_i$ is a vector from some reference point to the charge $q i$ . The value of $\mathbf{p}$ is independent of the choice of reference point, provided the overall charge of the system is zero. This expression is equivalent to the previous expression in the case where $N = 2$ . The fact that the dipole moment vector is directed from the negative charge to the positive charge is seen to be related to the fact that the plain position vector of a point is directed from the origin to that point.

For a continuous distribution of charge, the corresponding expression is:

$\mathbf{p} = \int\rho(\mathbf{r'})\, \mathbf{r'} \ d \tau'$

The dipole moment is most easily understood when the system has an overall neutral charge. For example, a pair of opposite charges, or a neutral conductor in a uniform electric field. For such systems, the value of the electric dipole moment is independent of the choice of reference point.

When discussing the dipole moment of a non-neutral system, such as the dipole moment of the proton, a dependence on the choice of reference point arises. In such cases it is conventional to choose the reference point to be center of mass of the system, not some arbitrary origin. This convention insures that the dipole moment is an intrinsic property of the system.