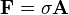Pressure
From Wikipedia, the free encyclopedia
Pressure (symbol: p) is the force per unit area applied on a surface in a direction perpendicular to that surface.
Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.
Contents
|
[edit] Definition
[edit] Formulaic
| Conjugate variables of thermodynamics | |
|---|---|
| Pressure | Volume |
| (Stress) | (Strain) |
| Temperature | Entropy |
| Chem. potential | Particle no. |
Mathematically:
where:
- p is the pressure,
- F is the normal force,
- A is the area.
Pressure is a scalar, and has SI units of pascals; 1 Pa = 1 N/m2.
Pressure is transmitted to solid boundaries or across arbitrary sections of fluid normal to these boundaries or sections at every point. It is a fundamental parameter in thermodynamics and it is conjugate to volume.
[edit] Units
The SI unit for pressure is the pascal (Pa), equal to one newton per square metre (N·m-2 or kg·m-1·s-2). This special name for the unit was added in 1971; before that, pressure in SI was expressed in units such as N/m2.
Non-SI measures (still in use in some parts of the world) include the pound-force per square inch (psi) and the bar.
The cgs unit of pressure is the barye (ba). It is equal to 1 dyn·cm-2.
Pressure is still sometimes expressed in mmHg/cm2 or grams-force/cm2 (sometimes as kg/cm2 and g/mol2 without properly identifying the force units). But using the names kilogram, gram, kilogram-force, or gram-force (or their symbols) as a unit of force is expressly forbidden in SI; the unit of force in SI is the newton (N). The technical atmosphere (symbol: at) is 1 kgf/cm2.
Some meteorologists prefer the hectopascal (hPa) for atmospheric air pressure, which is equivalent to the older unit millibar (mbar). Similar pressures are given in kilopascals (kPa) in practically all other fields, where the hecto prefix is hardly ever used. In Canadian weather reports, the normal unit is kPa. The obsolete unit inch of mercury (inHg, see below) is still sometimes used in the United States.
The standard atmosphere (atm) is an established constant. It is approximately equal to typical air pressure at earth mean sea level and is defined as follows.
- standard atmosphere = 101325 Pa = 101.325 kPa = 1013.25 hPa.
Because pressure is commonly measured by its ability to displace a column of liquid in a manometer, pressures are often expressed as a depth of a particular fluid (e.g., inches of water). The most common choices are mercury (Hg) and water; water is nontoxic and readily available, while mercury's density allows for a shorter column (and so a smaller manometer) to measure a given pressure. The pressure exerted by a column of liquid of height h and density ρ is given by the hydrostatic pressure equation p = ρgh.
Fluid density and local gravity can vary from one reading to another depending on local factors, so the height of a fluid column does not define pressure precisely. When millimetres of mercury or inches of mercury are quoted today, these units are not based on a physical column of mercury; rather, they have been given precise definitions that can be expressed in terms of SI units. The water-based units still depend on the density of water, a measured, rather than defined, quantity.
Although no longer favoured in physics, these manometric units are still encountered in many fields. Blood pressure is measured in millimetres of mercury in most of the world, and lung pressures in centimeters of water are still common. Scuba divers often use a manometric rule of thumb: the pressure exerted by ten metres depth of water is approximately equal to one atmosphere.
Other units presently or formerly in use include the following:
- atmosphere
- manometric units:
- centimetre, inch, and millimetre of mercury (torr)
- millimetre, centimetre, metre, inch, and foot of water
- imperial units:
- kip, ton-force (short), ton-force (long), pound-force, ounce-force, and poundal per square inch
- pound-force, ton-force (short), and ton-force (long)
- non-SI metric units:
- bar, millibar
- force, or kilopond, per square centimetre (technical atmosphere)
- gram-force and tonne-force (metric ton-force) per square centimetre
- barye (dyne per square centimetre)
- kilogram-force and tonne-force per square metre
- sthene per square metre (pieze)
pascal (Pa) | bar (bar) | technical atmosphere (at) | atmosphere (atm) | torr (mmHg) | pound-force per square inch (psi) | |
|---|---|---|---|---|---|---|
| 1 Pa | ≡ 1 N/m2 | 10−5 | 1.0197×10−5 | 9.8692×10−6 | 7.5006×10−3 | 145.04×10−6 |
| 1 bar | 100 000 | ≡ 106 dyn/cm2 | 1.0197 | 0.98692 | 750.06 | 14.504 |
| 1 at | 98 066.5 | 0.980665 | ≡ 1 kgf/cm2 | 0.96784 | 735.56 | 14.223 |
| 1 atm | 101 325 | 1.01325 | 1.0332 | ≡ 1 atm | 760 | 14.696 |
| 1 torr | 133.322 | 1.3332×10−3 | 1.3595×10−3 | 1.3158×10−3 | ≡ 1 mmHg | 19.337×10−3 |
| 1 psi | 6 894.76 | 68.948×10−3 | 70.307×10−3 | 68.046×10−3 | 51.715 | ≡ 1 lbf/in2 |
Example reading: 1 Pa = 1 N/m2 = 10−5 bar = 10.197×10−6 at = 9.8692×10−6 atm, etc.
Note: mmHg is an abbreviation for millimetres of mercury.
[edit] Examples
As an example of varying pressures, a finger can be pressed against a wall without making any lasting impression; however, the same finger pushing a thumbtack can easily damage the wall. Although the force applied to the surface is the same, the thumbtack applies more pressure because the point concentrates that force into a smaller area. Pressure is transmitted to solid boundaries or across arbitrary sections of fluid normal to these boundaries or sections at every point. Unlike stress, pressure is defined as a scalar quantity.
The gradient of pressure is called the force density. For gases, pressure is sometimes measured not as an absolute pressure, but relative to atmospheric pressure; such measurements are called gauge pressure (also sometimes spelled gage pressure).[1] An example of this is the air pressure in an automobile tire, which might be said to be "220 kPa", but is actually 220 kPa above atmospheric pressure. Since atmospheric pressure at sea level is about 100 kPa, the absolute pressure in the tire is therefore about 320 kPa. In technical work, this is written "a gauge pressure of 220 kPa". Where space is limited, such as on pressure gauges, name plates, graph labels, and table headings, the use of a modifier in parentheses, such as "kPa (gauge)" or "kPa (absolute)", is permitted. In non-SI technical work, a gauge pressure is sometimes written as "32 psig", though the other methods explained above that avoid attaching characters to the unit of pressure are preferred.[2]
Gauge pressure is a critical measure of pressure wherever one is interested in the stress on storage vessels and the plumbing components of fluidics systems. However, whenever equation-of-state properties, such as densities or changes in densities, must be calculated, pressures must be expressed in terms of their absolute values. For instance, at an altitude of 112 m, the mean atmospheric pressure is 100 kPa. At this altitude, a pressure vessel containing any gas (such as helium) at 200 kPa (gauge), or 300 kPa (absolute), is 50 % more dense than at 100 kPa (gauge), 200 kPa (absolute); not double the density, as one might assume by focusing on gauge values.
[edit] Scalar nature
In a static gas, the gas as a whole does not appear to move. The individual molecules of the gas, however, are in constant random motion. Because we are dealing with an extremely large number of molecules and because the motion of the individual molecules is random in every direction, we do not detect any motion. If we enclose the gas within a container, we detect a pressure in the gas from the molecules colliding with the walls of our container. We can put the walls of our container anywhere inside the gas, and the force per unit area (the pressure) is the same. We can shrink the size of our "container" down to an infinitely small point, and the pressure has a single value at that point. Therefore, pressure is a scalar quantity, not a vector quantity. It has a magnitude but no direction associated with it. Pressure acts in all directions at a point inside a gas. At the surface of a gas, the pressure force acts perpendicular to the surface.
A closely related quantity is the stress tensor σ, which relates the vector force F to the vector area A via
This tensor may be divided up into a scalar part (pressure) and a traceless tensor part shear. The shear tensor gives the force in directions parallel to the surface, usually due to viscous or frictional forces. The stress tensor is sometimes called the pressure tensor, but in the following, the term "pressure" will refer only to the scalar pressure.
[edit] Types
[edit] Explosion or Deflagration Pressures
Explosion or deflagration pressures are the result of the ignition of explosible gases, mists, dust/air suspensions, in unconfined and confined spaces.
[edit] Negative pressures
While pressures are generally positive, there are several situations in which a negative pressure may be encountered:
- When dealing in relative (gauge) pressures. For instance, an absolute pressure of 80 kPa may be described as a gauge pressure of -21 kPa (i.e., 21 kPa below an atmospheric pressure of 101 kPa).
- When attractive forces (e.g., Van der Waals forces) between the particles of a fluid exceed repulsive forces. Such scenarios are generally unstable since the particles will move closer together until repulsive forces balance attractive forces. Negative pressure exists in the transpiration pull of plants.
- The Casimir effect can create a small attractive force due to interactions with vacuum energy; this force is sometimes termed 'vacuum pressure' (not to be confused with the negative gauge pressure of a vacuum).
- Depending on how the orientation of a surface is chosen, the same distribution of forces may be described either as a positive pressure along one surface normal, or as a negative pressure acting along the opposite surface normal.
- In the cosmological constant.
[edit] Hydrostatic pressure (head pressure)
Hydrostatic pressure is the pressure due to the weight of a fluid.
where:
- ρ (rho) is the density of the fluid (i.e., the practical density of fresh water is 1000 kg/m3);
- g is the acceleration due to gravity (approximately 9.81 m/s2 on earth's surface);
- h is the height of the fluid column (in metres). Feet can be used if the rest of the units used in the equation are defined in feet.
See also Pascal's law.
[edit] Stagnation pressure
Stagnation pressure is the pressure a fluid exerts when it is forced to stop moving. Consequently, although a fluid moving at higher speed will have a lower static pressure, it may have a higher stagnation pressure when forced to a standstill. Static pressure and stagnation pressure are related by the Mach number of the fluid. In addition, there can be differences in pressure due to differences in the elevation (height) of the fluid. See Bernoulli's equation (note: Bernoulli's equation only applies for incompressible flow).
The pressure of a moving fluid can be measured using a Pitot probe, or one of its variations such as a Kiel probe or Cobra probe, connected to a manometer. Depending on where the inlet holes are located on the probe, it can measure static pressure or stagnation pressure.
[edit] Surface pressure
There is a two-dimensional analog of pressure -- the lateral force per unit length applied on a line perpendicular to the force.
Surface pressure is denoted by π and shares many similar properties as three-dimensional pressure. Properties of surface chemicals can be investigated by measuring pressure/area isotherms, as the two-dimensional analog of Boyle's law, πA = k, at constant temperature.