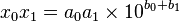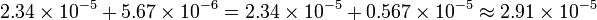Scientific notation

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Scientific notation, also known as standard form, is a notation for writing numbers that is often used by scientists and mathematicians to make it easier to write large and small numbers. A number that is written in scientific notation has several properties that make it very useful to scientists.

1 Variations
- 1.1 Normalized notation
- 1.2 E notation
- 1.3 Engineering notation
- 1.4 Usage of spaces
2 Motivation
- 2.1 Examples
- 2.2 Significant figures
- 2.3 Order of magnitude
3 Using scientific notation
- 3.1 Converting
- 3.2 Basic operations
4 References
5 External links

[edit] Variations

The basic concept for the practical notations is this mathematical exponential expression using powers of ten :

$a\,\times\,10^b\!$

wherein exponent b is an integer, and the coefficient a any real number, called the significand or mantissa (using "mantissa" may cause confusion as it can also refer to the fractional part of the common logarithm).

[edit] Normalized notation

Written in the form a × 10^b, exponent b is chosen such that the absolute value of a remains at least one but less than ten 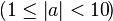$(1 \le \left | a \right \vert < 10\!)$ . Normal mathematics convention dictates a minus sign to precede the first of the decimal digits of a for a negative number; that of b for a number with absolute value between 0 and 1, e.g. minus one half is −5 × 10⁻¹. There is no need to represent zero in normalized form, the digit 0 suffices. The normalized form allows easy comparison of two numbers of the same sign in a, as the exponent b gives the number's order of magnitude.

It is implicitly assumed that scientific notation should always be normalized except during calculations or when an unnormalized form, such as engineering notation, is desired. (Normalized) scientific notation is often called exponential notation — though the latter term is more general as it applies as well, for instance, to engineering notation or any value for a and to bases other than 10 like 315 × 2²⁰.

[edit] E notation

Most calculators and many computer programs present very large and very small results in scientific notation. Because exponents like 10⁷ can't always be conveniently represented on computers, typewriters, and calculators, an alternate notation is often used: the letter "E" or "e" is used for "times ten raised to the power", thus replacing the "×10ⁿ" while the exponent is not superscripted but is left on the same level with the significand (e.g. a E−6 not a E⁻⁶). The sign is often given even if positive (e.g. a E+11 rather than a E11). For example, 6.0221415 E+23 or 6.0221415 e23 is the same as 6.0221415 × 10²³(Avogadro's number). Note that this character "e" is not related to the mathematical constant e (a confusion not possible when using capital "E") ; and though it is short for exponent, the notation is referred to as (scientific) E notation or (scientific) e notation rather than (scientific) exponential notation though the latter also occurs. The E notation is a variant representation that strictly meets the mathematical requirements of the normalized notation. Examples:

In the FORTRAN programming language 6.0221415E23 is equivalent to 6.0221415 × 10²³.
The ALGOL^[1]^[2] programming language also uses the E notation, alternatively - when available - either character '₁₀' or '\' can be used, for example: 6.0221415₁₀23 and 6.0221415\23.

[edit] Engineering notation

Engineering notation differs from the normalized exponential notation by restricting the exponent b to multiples of 3. Consequently, the absolute value of a can need to be equal or larger than 10 (ranging from 1 to limit 1,000) and thus engineering notation does not meet the conditions set for the normalized form, and is rarely called scientific notation. Numbers in this form are easily read out using magnitude prefixes like mega- (b=6), kilo- (b=3), milli- (b=-3), micro- (b=-6) or nano- (b=-9). For example, 12.5 × 10⁻⁹ m can be read as "twelve point five nanometers" or written as 12.5 nm.

[edit] Usage of spaces

In scientific normalized exponential notation, in E notation, and in engineering notation, the space (which in typesetting may be represented with a normal width space or a thin space) that is allowed only before and after "×" or in front of "E" or "e", may as well be omitted though it is less common to disappear from before the alphabetical character.^[3]

[edit] Motivation

Scientific notation is a very convenient way to write large or small numbers and do calculations with them. It also quickly conveys two properties of a measurement that are useful to scientists—significant figures and order of magnitude.

[edit] Examples

An electron's mass is about 0.000 000 000 000 000 000 000 000 000 000 910 938 26 kg. In scientific notation, this is written 9.1093826×10⁻³¹ kg.
The Earth's mass is about 5,973,600,000,000,000,000,000,000 kg. In scientific notation, this is written 5.9736×10²⁴ kg.
The Earth's circumference is approximately 40,000,000 m (i.e. 4 followed by 7 zeroes). In scientific notation, this is written 4×10⁷ m. In engineering notation, this is written 40×10⁶ m. In SI writing style, this may be written "40 Mm" ("40 megameters").

[edit] Significant figures

It is a common mistake to confuse scientific notation with the idea of significant figures. In fact, scientific notation does not require using significant figures, nor vice versa.

For example, using scientific notation, in SI units the speed of light is 2.99792458×10⁸ m/s and the inch is 2.54×10^-2 m. It would be a mistake to assume that either of these expressions indicated any uncertainty; in fact both numbers are exact.^[4]

It is possible to use scientific notation in conjunction with significant figures, but this is not mandatory and should never be assumed. It is always better to state the uncertainty explicitly. For instance, the accepted value of the unit of elementary charge can properly be expressed as 1.602176487(40)×10^-19 coulomb,^[5] where the (40) indicates 40 counts of uncertainty in the last decimal place. If a number has been rounded off, it can be written in the form 2.5(½)×10^-2 to explicitly indicate that there is a half-count of uncertainty in the last digit.

[edit] Order of magnitude

Scientific notation also enables simple order of magnitude comparisons. A proton's mass is 0.000 000 000 000 000 000 000 000 001 672 6 kg. If this is written as 1.6726×10⁻²⁷ kg, it is easier to compare this mass with that of the electron, given above. The order of magnitude of the ratio of the masses can be obtained by simply comparing the exponents rather than counting all the leading zeros. In this case, '−27' is larger than '−31' and therefore the proton is four orders of magnitude (about 10,000 times) more massive than the electron.

Scientific notation also avoids misunderstandings due to regional differences in certain quantifiers, such as 'billion', which might indicate either 10⁹ or 10¹².

[edit] Using scientific notation

[edit] Converting

Multiplication and division by 10 are easy to perform in decimal scientific notation.

At the mantissa, multiplication by 10 may be seen as shifting the decimal separator one position to the right (adding a zero if needed): 12.34×10=123.4. Division may be seen as shifting it to the left: 12.34/10=1.234

In the exponential part multiplication by 10 results in adding 1 to the exponent: 10²×10=10³. Division by 10 results in subtracting 1 from the exponent: 10²/10=10¹.

Also notice that 1 is multiplication's neutral element and that 10⁰=1.

To convert between different representations of the same number, all that is needed is to perform the opposite operations to each part. Thus multiplying the mantissa by 10, n times is done by shifting the decimal separator n times to the right. Dividing by 10 the same number of times is done by adding −n to the exponent. Some examples:

$123.4 = 123.4\times10^0 = (123.4/10^2) \times (10^0\times10^2) = 1.234\times10^2$

$0.001234 = 0.001234\times10^0 = (0.001234\times 10^3) \times (10^0 / 10^3) = 1.234\times10^{-3}$

[edit] Basic operations

Given two numbers in scientific notation,

$x_0=a_0\times10^{b_0}$

$x_1=a_1\times10^{b_1}$

Multiplication and division are performed using the rules for operation with exponential functions:

$x_0 x_1=a_0 a_1\times10^{b_0+b_1}$

$\frac{x_0}{x_1}=\frac{a_0}{a_1}\times10^{b_0-b_1}$

some examples are:

$5.67\times10^{-5} \times 2.34\times10^2 \approx 13.3\times10^{-3} = 1.33\times10^{-2}$

$\frac{2.34\times10^2}{5.67\times10^{-5}} \approx 0.413\times10^{7} = 4.13\times10^6$

Addition and subtraction require the numbers to be represented using the same exponential part, in order to simply add, or subtract, the mantissas, so it may take two steps to perform. First, if needed, convert one number to a representation with the same exponential part as the other. This is usually done with the one with the smaller exponent. Second, add or subtract the mantissas.

$x_1^\star = a_1^\star \times10^{b_0}$

$x_0 \pm x_1=x_0 \pm x_1^\star=(a_0\pm a_1^\star)\times10^{b_0}$

an example:

$2.34\times10^{-5} + 5.67\times10^{-6} = 2.34\times10^{-5} + 0.567\times10^{-5} \approx 2.91\times10^{-5}$