9 (number)

From Wikipedia, the free encyclopedia

Jump to: navigation, search

This article is about the number. For other uses, see 9 (disambiguation).

This article needs additional references or sources for verification.
Please help to improve this article by adding reliable references. Unverifiable material may be challenged and removed.
This article has been tagged since August 2007.

0 1 2 3 4 5 6 7 8 9 → List of numbers — Integers 0 10 20 30 40 50 60 70 80 90 →
Cardinal	9 nine
Ordinal	9th ninth
Numeral system	novenary
Factorization	$32$
Divisors	1, 3, 9
Roman numeral	IX
Roman numeral (Unicode)	Ⅸ, ⅸ
prefixes	ennea- (from Greek) nona- (from Latin)
Binary	1001
Octal	11
Duodecimal	9
Hexadecimal	9
Arabic-Indic numeral	٩
Armenian numeral	Թ
Bengali	৯
Chinese/Japanese numeral	九玖 (formal writing)
Devanāgarī	९
Greek numeral	θ´
Hebrew numeral	ט (Tet)
Tamil numeral	௯
Khmer	៩
Thai numeral	๙

Look up nine in
Wiktionary, the free dictionary.

9 (nine) is the natural number following 8 and preceding 10.

1 In mathematics
- 1.1 In numeral systems
- 1.2 List of basic calculations
2 Evolution of the glyph
3 In science
- 3.1 Astronomy
- 3.2 Probability
4 In religion
5 As lucky or unlucky number
6 In music
7 In sports
8 In technology
9 Nine and the circle
10 In other fields
11 References
12 See also
13 Historical years

[edit] In mathematics

Nine is a composite number, its proper divisors being 1 and 3. It is 3 times 3 and hence the third square number. 9 is a Motzkin number. It is the first composite lucky number.

9 is the second non-unitary square prime (3^2). It has a unique aliquot sum σ(n) 4 which is itself a square prime. 9 is the only square prime with an aliquot sum of the same form. The aliquot sequence of 9 has 5 members (9,4,3,1,0) this number being the 2nd composite member of the 3-aliquot tree.

There are nine Heegner numbers.

Since $9 = 3^{2^1}$ , 9 is an exponential factorial.

8 and 9 form a Ruth-Aaron pair under the second definition that counts repeated prime factors as often as they occur.

A polygon with nine sides is called an enneagon (technically) or nonagon (in common usage). A group of nine of anything is called an ennead.

In base 10 a number is evenly divisible by nine if and only if its digital root is 9. That is, if you multiply nine by any whole number (except zero), and repeatedly add the digits of the answer until it's just one digit, you will end up with nine:

2 × 9 = 18 (1 + 8 = 9)
3 × 9 = 27 (2 + 7 = 9)
9 × 9 = 81 (8 + 1 = 9)
121 × 9 = 1089 (1 + 0 + 8 + 9 = 18; 1 + 8 = 9)
234 × 9 = 2106 (2 + 1 + 0 + 6 = 9)
578329 × 9 = 5204961 (5 + 2 + 0 + 4 + 9 + 6 + 1 = 27 (2 + 7 = 9))
482729235601 × 9 = 4344563120409 (4 + 3 + 4 + 4 + 5 + 6 + 3 + 1 + 2 + 0 + 4 + 0 + 9 = 45 (4 + 5 = 9))
(Exception) 0 x 9 = 0 (0 is not equal to 9)

The only other number with this property is three. In base N, the divisors of N − 1 have this property. Another consequence of 9 being 10 − 1, is that it is also a Kaprekar number.

The difference between a base-10 positive integer and the sum of its digits is a whole multiple of nine. Examples:

The sum of the digits of 41 is 5, and 41-5 = 36. The digital root of 36 is 3+6 = 9, which, as explained above, demonstrates that it is evenly divisible by nine.
The sum of the digits of 35967930 is 3+5+9+6+7+9+3+0 = 42, and 35967930-42 = 35967888. The digital root of 35967888 is 3+5+9+6+7+8+8+8 = 54, 5+4 = 9.

Subtracting two base-10 positive integers that are transpositions of each other yields a number that is a whole multiple of nine. Some examples:

41-14 = 27. The digital root of 27 is 2+7 = 9.
36957930-35967930 = 990000, which is obviously a multiple of nine.

This works regardless of the number of digits that are transposed. For example, the largest transposition of 35967930 is 99765330 (all digits in descending order) and its smallest transposition is 03356799 (all digits in ascending order); subtracting pairs of these numbers produces:

99765330-35967930 = 63797400; 6+3+7+9+7+4+0+0 = 36, 3+6 = 9.
99765330-03356799 = 96408531; 9+6+4+0+8+5+3+1 = 36.
35967930-03356799 = 32611131; 3+2+6+1+1+1+3+1 = 18, 1+8 = 9.

Casting out nines is a quick way of testing the calculations of sums, differences, products, and quotients of integers.

Every prime in a Cunningham chain of the first kind with a length of 4 or greater is congruent to 9 mod 10 (the only exception being the chain 2, 5, 11, 23, 47).

Six recurring nines appear in the decimal places 762 through 767 of pi. This is known as the Feynman point (see also MathWorld).

If an odd perfect number is of the form 36k+9, it has at least nine distinct prime factors.

Nine is the binary complement of number six:

 9 = 1001 6 = 0110

[edit] In numeral systems

Base	Numeral system
2	binary	1001
3	ternary	100
4	quaternary	21
5	quinary	14
6	senary	13
7	septenary	12
8	octal	11
9	novenary	10
over 9 (decimal, hexadecimal)		9

One billion is a number that contains nine zeros.

[edit] List of basic calculations

Multiplication	1	2	3	4	5	6	7	8	9	10		11	12	13	14	15	16	17	18	19	20		21	22	23	24	25		50	100	1000
$9 \times x$	9	18	27	36	45	54	63	72	81	90		99	108	117	126	135	144	153	162	171	180		189	198	207	216	225		450	900	9000

Division	1	2	3	4	5	6	7	8	9	10		11	12	13	14	15
$9 \div x$	9	4.5	3	2.25	1.6	1.5	$1.\overline{285714}$	1.125	1	0.9		$0.\overline{8}\overline{1}$	0.75	$0.\overline{692307}$	$0.6\overline{428571}$	0.6
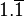$x \div 9$	$0.\overline{1}$	$0.\overline{2}$	$0.\overline{3}$	$0.\overline{4}$	$0.\overline{5}$	$0.\overline{6}$	$0.\overline{7}$	$0.\overline{8}$	1	$1.\overline{1}$		$1.\overline{2}$	$1.\overline{3}$	$1.\overline{4}$	$1.\overline{5}$	$1.\overline{6}$

Exponentiation	1	2	3	4	5	6	7	8	9	10		11	12	13
$9 ^ x\,$	9	81	729	6561	59049	531441	4782969	43046721	387420489	3486784401		31381059609	282429536481	2541865828329
$x ^ 9\,$	1	512	19683	262144	1953125	10077696	40353607	134217728	387420489	1000000000		2357947691	5159780352	10604499373

Radix	1	5	10	15	20	25	30	40	50	60	70	80	90	100
Radix	110	120	130	140	150	200	250	500	1000	10000	100000	1000000
$x_{9} \$	1	5	$11_{9} \$	$16_{9} \$	$22_{9} \$	$27_{9} \$	$33_{9} \$	$44_{9} \$	$55_{9} \$	$66_{9} \$	$77_{9} \$	$88_{9} \$	$110_{9} \$	$121_{9} \$
$x_{9} \$	$132_{9} \$	$143_{9} \$	$154_{9} \$	$165_{9} \$	$176_{9} \$	$242_{9} \$	$307_{9} \$	$615_{9} \$	$1331_{9} \$	$14641_{9} \$	$162151_{9} \$	$1783661_{9} \$

[edit] Evolution of the glyph

According to Georges Ifra, the origin of the 9 integers can be attributed to the ancient Indian civilization, and was adopted by subsequent civilizations in conjunction with the 0.^[1]

In the beginning, various Indians wrote 9 similar to the modern closing question mark without the bottom dot. The Kshtrapa, Andhra and Gupta started curving the bottom vertical line coming up with a 3-look-alike. The Nagari continued the bottom stroke to make a circle and enclose the 3-look-alike, in much the same way that the @ character encircles a lowercase a. As time went on, the enclosing circle became bigger and its line continued beyond the circle downwards, as the 3-look-alike became smaller. Soon, all that was left of the 3-look-alike was a squiggle. The Arabs simply connected that squiggle to the downward stroke at the middle and subsequent European change was purely cosmetic.

While the shape of the 9 character has an ascender in most modern typefaces, in typefaces with text figures the character usually has a descender, as, for example, in .

[edit] In science

Nine is the atomic number of fluorine.

[edit] Astronomy

Before 2006 (when Pluto was officially designated as a non-planet), there were nine planets in the solar system.
Messier object M9 is a magnitude 9.0 globular cluster in the constellation Ophiuchus.
The New General Catalogue object NGC 9, a spiral galaxy in the constellation Pegasus

The Saros number of the solar eclipse series which began on -2568 February 6 and ended on -1252 April 4. The duration of Saros series 9 was 1316.2 years, and it contained 74 solar eclipses.
The Saros number of the lunar eclipse series which began on -2501 June 26 and ended on -1149 September 16. The duration of Saros series 9 was 1352.2 years, and it contained 76 lunar eclipses.

[edit] Probability

In probability, the nine is a logarithmic measure of probability of an event, defined as the negative of the base-10 logarithm of the probability of the event's complement. For example, an event that is 99% likely to occur has an unlikelihood of 1% or 0.01, which amounts to −log₁₀ 0.01 = 2 nines of probability. Zero probability gives zero nines (−log₁₀ 1 = 0). The purity of chemicals (see Nine (purity)), the effectivity of processes, the availability of systems etc. can similarly be expressed in nines. For example, "five nines" (99.999%) availability implies a total downtime of no more than five minutes per year. This measure can be confusing, a fact which is discussed in the myth of the nines.

[edit] In religion

Important Buddhist rituals usually involve nine monks.
The first nine days of the Hebrew month of Av are collectively known as "The Nine Days" (Tisha HaYamim), and are a period of semi-mourning leading up to Tisha B'Av, the ninth day of Av on which both Temples in Jerusalem were destroyed.
Nine, as the highest single-digit number (in base ten), symbolizes completeness in the Bahá'í Faith. In addition, the word Bahá' in the Abjad notation has a value of 9, and a 9-pointed star (Enneagram) is used to symbolize the religion.

[edit] As lucky or unlucky number

Nine (九 pinyin jiǔ) is considered a good number in Chinese culture because it sounds the same as the word "longlasting" (久 pinyin jiǔ). The Japanese consider 9 to be unlucky, however, because it sounds similar to the Japanese word for "pain" or "distress" (苦 kunrei ku).

Nine is strongly associated with the Chinese dragon, a symbol of magic and power. There are nine forms of the dragon, it is described in terms of nine attributes, and it has nine children It has 9×13 scales, 9×9 being yang (masculine, or bad influence) and 9×4 being yin (feminine, or good influence).^[2]

[edit] In music

In music theory a ninth is the ninth note of a musical scale or the interval between the first note and the ninth. A ninth chord is a chord with a ninth.

In classical music the curse of the ninth refers to the superstition that a composer who writes a ninth symphony will die soon. Beethoven, who left his Tenth Symphony unfinished, is regarded by the superstition as the first victim of the curse.

Bands with the number nine in their name include Nine,Stroke 9, Nine Days, and Nine Inch Nails.

The Beatles released a song called "Revolution 9" which appears on The White Album (more properly known as The Beatles); its principal vocal feature is a voice repeating, "Number nine...number nine...number nine..." John Lennon, the primary composer of "Revolution 9", also released a solo recording entitled "#9 Dream". The Beatles also released a song called "One After 909" in 1970, although it was recorded in 1969, and Lennon and McCartney had worked on it since the very early days. Lennon is known to have felt a connection with the number 9. Both he and his son, Sean were born on October 9^th. Also, John died on the 9^th (UK Time). Ironically, of all the Beatles' singles that made the U.S. Top 10 in Billboard, all peak positions were covered except #9.

The first single of Leeds-based band ¡Forward, Russia! was called Nine and was released in April 2005. The title did not carry any symbolism, but followed the then "tradition" of the band for naming their songs in the order in which they were written.

Composer Maury Yeston adapted Federico Fellini's 8½ for Broadway as the musical Nine, which won several Tony Awards in 1982, and was successfully revived in 2003 starring Antonio Banderas.
Roger Miller had a hit with the song "Engine Engine Number Nine."

9 is also the name of various albums, including 9 by Mercyful Fate, released in 1999, and 9 by Public Image Limited. Fairport Convention also released an album with the number for a title. Irish singer/songwriter Damien Rice released an album called 9 in November 2006.

In urban culture, 'nine' is a slang word for a 9mm pistol or homicide, the latter from the Illinois Criminal Code for homicide.

Rock band Linkin Park released a song in their album Meteora called "Figure.09"

In hip-hop, the rapper Nine, who got his big break in late 1993 as a featured guest on First Funkmaster Flex and the Ghetto Celebs, released 2 albums (Nine Livez in 1995 and Cloud Nine in 1996) and is now making a comeback.[1]

[edit] In sports

Nine ball is the standard professional pocket billiards variant played in the United States.
In football the centre-forward/striker commonly wears the number 9 shirt. The number was made most famous by Ronaldo and has also been used by other famous strikers such as Hernan Crespo and Samuel Eto'o.
The car number of the 1988 NASCAR Nextel Cup championship-winning team, when Bill Elliott won the title. He used this number again from 2001 to 2003. Kasey Kahne has driven the 9 car since 2004.
In baseball, nine represents the right fielder's position.
The retired uniform numbers of former baseball players Ted Williams and Roger Maris. Reggie Jackson also wore 9 with the Oakland A's for nine years and is now retired.
In ice hockey the number 9 is one of the most prestigious sweater numbers, having been worn by legends like Maurice Richard, Bobby Hull, and Gordie Howe. It was also worn, doubled as 99, by the great Wayne Gretzky.
In association football players that wear the number 9 are key players in the offense and likely to score many goals.
Famed football(soccer) player Ronaldo (Brazilian men's national team) wears #9.
The San Francisco 49ers are sometimes referred to as the "niners".
The most notable NFL quarterbacks to ever wear the number 9 are Drew Brees of the New Orleans Saints, Carson Palmer of the Cincinnati Bengals, Tony Romo of the Dallas Cowboys and Steve McNair of the Baltimore Ravens.
The number worn by current NBA player Tony Parker of the San Antonio Spurs, MVP of the 2007 NBA Finals.

[edit] In technology

ISO 9 is the ISO's standard for the transliteration of Cyrillic characters into Latin characters
In the Rich Text Format specification, 9 is the language code for the English language. All codes for regional variants of English are congruent to 9 mod 256.

In computer system administration, uptime, a measure of the time a computer system has been up and running, is sometimes measured in "nines"—that is, the number of "9" digits in the percentage of time the computer is normally running. For example, "five nines" means 99.999% reliability, which translates to a total downtime of no longer than five minutes per year.

[edit] Nine and the circle

The Enneagram is one system of knowledge which shows the correspondence between the 9 integers and the circle. The 360 degrees of the circle, which can be trace back to the Rig Veda of ancient India, can also be seen to speak of the 9, via theosophical addition (3 + 6 + 0 = 9)[2]. [2]

[edit] In other fields

International maritime signal flag for 9

Playing cards showing the 9 of all four suits

Nine is the highest single-digit number in the decimal system.
In the NATO phonetic alphabet, the digit 9 is called "niner".
Channel 9, an Australian free-to-air television station
Nine judges sit on the United States Supreme Court.
The word "K-9" pronounces the same as canine and is used in many U.S. police departments to denote the unit working with police dog.
The ordinal adjective is ninth.
Stanines are measured on a scale of 1 to 9.
The name of the area called Kowloon in Hong Kong literally means: nine dragons.
Someone dressed "to the nines" is dressed up as much as they can be.
Nine Lives Cat Food got its name from the legend that a cat has nine lives.
Nine rank system
The Nine Chapters on the Mathematical Art
Nine Worthies
9: The Last Resort was a 1995 computer game.
Seven of Nine, fictional character from the Star Trek universe
Magic: The Gathering has a set of nine rare cards, widely regarded as overpowered, known as the Power Nine.
Nine West is a popular brand for clothing.
The number of hostages in the TV show The Nine
Ninth Avenue is a major avenue in Manhattan.
Nine Unknown Men are, in occult legend, the custodians of the sciences of the world since ancient times.
The 9, a show on the Internet, hosted by Maria Sansone. The 9
The Nines is a film written and directed by John August, starring Ryan Reynolds, Hope Davis and Melissa McCarthy. It is scheduled to premiere at the 2007 Sundance Film Festival.
In the game of Craps, 9 is known as the center field because it is in the middle of the seven numbers on the field bet.
"A cat-o'-nine-tails suggests perfect punishment and atonement." --Robert Ripley.
Wally Cleaver's locker number was #9.