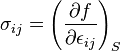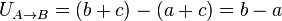Potential energy

From Wikipedia, the free encyclopedia

Jump to: navigation, search

Energy Portal

Potential energy is energy stored within a Physical system. Informally, it exists when there is a force which tends to pull an object back towards some original position when it is moved. For example, a spring can be stretched and held, or a weight can be lifted against gravity and suspended. Both of these actions require energy to perform. The principle of conservation of energy says that energy can neither be created or destroyed, so this energy does not disappear. Instead it is stored as potential energy. If the spring is released or the weight is dropped, this stored energy will reappear as kinetic energy as the restoring force -- elasticity in the case of the spring and gravity in the case of the weight -- accelerates the object back towards its original position.

There are a number of different types of potential energy, each associated with a particular kind of force. Technically, any conservative force gives rise to potential energy. For example, the work of elastic force is called elastic potential energy; work of gravitational force is called gravitational potential energy, work of the Coulomb force is called electric potential energy; work of strong nuclear force or weak nuclear force acting on the baryon charge is called nuclear potential energy; work of intermolecular forces is called intermolecular potential energy. Chemical potential energy, such as the energy stored in fossil fuels, is the work of Coulomb force during rearrangement of mutual positions of electrons and nuclei in atoms and molecules. Thermal energy usually has two components: the kinetic energy of random motion of particles and potential energy of their mutual positions.

The phrase 'potential energy' was coined by William Rankine.^[1]

1 Gravitational potential energy
2 Calculation of gravitational potential energy
- 2.1 Gravitational potential
3 Elastic potential energy
- 3.1 Calculation of elastic potential energy
4 Chemical potential energy
5 Electrical potential energy
- 5.1 Electrostatic potential energy
- 5.2 Electrodynamic potential energy
- 5.3 Nuclear potential energy
6 Thermal potential energy
7 Rest mass energy
8 Relation between potential energy and force
9 References

[edit] Gravitational potential energy

Gravitational potential energy is the work of gravitational force (usually taken with negative sign due to path convention).

The gravitational force keeps the planets in orbit about the Sun.

For example, consider a book, placed on top of a table. When the book is raised from the floor to the table, the gravitational force does negative work. If the book is returned back to the floor, the exact same (but positive) work will be done by the gravitational force. Thus, if the book is knocked off the table, this work (called potential energy) goes to accelerate the book (and now is called kinetic energy). When the book hits the floor this kinetic energy is converted into heat and sound by the impact.

The factors that affect an object's gravitational potential energy are the height to which it is raised, its mass, and the strength of the gravitational field in which it is raised. Thus, a book lying on a table has less gravitational potential energy than the same book on top of a taller cupboard, and less gravitational potential energy than a heavier book lying on the same table. An object at a certain height above the Moon's surface has less gravitational potential energy than at the same height on Earth because the Moon's gravity is weaker. (The gravitational force between any two objects is directly proportional to the product of their masses and inversely proportional to the square of the distance between them, according to Newton's law of gravitation.)

[edit] Calculation of gravitational potential energy

The work of gravitational force in raising an object (taken with the negative sign) is equal to the negative of the force applied multiplied by the distance through which the object is raised:

$U_g = -(- m g) h = mgh \,$

where

m is the mass of the object

g is the standard gravity (approximately 9.8 m/s² at the earth's surface)

h is the height to which the object is raised, relative to a given reference level (such as the earth's surface).

When applying this equation it is essential to use consistent units. Most scientific work is now done in SI units, in which case mass is measured in kilograms (kg), acceleration in meters per second squared (m/s²), and distance (here height) in meters (m). The resulting energy is expressed in joules (kg m²/s²).

The equation shows that gravitational potential energy is proportional to both mass and height. For example, raising two similar objects, or raising the same object twice as far, doubles the potential energy.

The "mgh" formula works well provided that the acceleration due to gravity, g, is very nearly constant over the distance h. On or close to the surface of the earth this assumption is reasonable, but over the much larger distances applying, for example, to spacecraft and astronomical bodies, it is not.

To calculate gravitational potential energy with varying g it is necessary to sum all the individual increments of potential energy as the masses are separated, taking account of the varying value of g as we go. In the limit, as the increments become "infinitely small", the sum becomes an integral.

To simplify the evaluation of the integral we can make the assumption that the gravitational forces act as if the objects' masses were concentrated at their respective centers of mass. This assumption is mathematically exactly correct for a spherically symmetrical object (such as, to a reasonable approximation, a planet). It is not generally correct in other cases, though if the dimensions of an object are very small compared to the distance of separation then it is reasonable to consider it as a point mass and ignore the details of its shape.

With this simplifying assumption, integrating force over distance leads to the following general expression for the gravitational potential energy, U_g, of a system of two masses:

	$U_g\,$	$= \int_{h_1}^{h_2} {G m_1 m_2 \over r^2} dr$
		$= G m_1 m_2 \left ( \frac{1}{h_1} - \frac{1}{h_2} \right )$

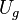where

m 1

and

m 2

are the masses of the two objects

G

is the gravitational constant, 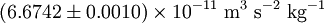$\left(6.6742 \plusmn 0.0010 \right) \times 10^{-11} \ \mbox{m}^3 \ \mbox{s}^{-2} \ \mbox{kg}^{-1} \,$ , (not to be confused with the g used earlier)

h 1

is the reference level (the separation at which potential energy is considered to be zero)

h 2

is the actual distance between the objects.

Subject to the caveats mentioned above, the distances $h 1$ and $h 2$ are measured between the objects' centres of mass.

For example, in the case of a small object above the surface of the earth, with reference level at the surface, $m 1$ and $m 2$ are respectively the masses of the earth and the object, $h 1$ is the distance from the earth's centre to the earth's surface, and $h 2$ is the distance from the earth's centre to the object.

If we try to calculate an "absolute" potential energy by setting the reference level at zero then the formula "blows up" with division by zero. In other words, we can only actually use this formula to measure the difference in potential energy between one non-zero separation and another.

In practice it is often convenient to take the reference level at infinite separation (i.e. $h_1 = \infty$ ), in which case the formula becomes:

$U_g = \frac{-G m_1 m_2}{r}$

where r is now the distance between the centres of mass of the two objects (again noting the earlier caveats). For a small object above the surface of the earth, r is the distance from the object to the earth's centre (and similarly for other spherical bodies).

Using this convention, potential energy is zero when r is infinitely large, and negative at any finite r. However, the difference in potential energy at different values of r – the quantity we are actually interested in – takes the expected sign.

U_g as calculated above measures the potential energy of the whole system. This can be visualised as if two bodies in space were released from rest and allowed to come together under the force of gravity. The sum of the kinetic energy gained by the two objects is exactly equal to the decrease in the potential energy of the system. The ratio of the objects' individual kinetic energy gains is equal to the reciprocal of the ratio of their masses. So, in the case of a relatively light object falling towards a very massive object (such as the earth), the contribution from the massive object is insignificant. In some sense, therefore, we can say that almost all the potential energy of the system is embodied in the light object, and almost none in the very massive object.

See also two-body problem and gravitational binding energy.

[edit] Gravitational potential

Gravitational potential is the potential energy per unit mass of an object due to its position in a gravitational field. The gravitational potential due to a point mass:

$E(r) = \frac{-Gm}{r} \$

where:

$G \$ is the universal gravitational constant,
$r \$ is the distance to the center of mass of the object,
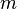$m \$ is the mass of the point object.

In astrodynamics the gravitational potential function has to account for the non-spherical and non-homogeneous nature of typical sources of gravitational potential. In this case a gravitational potential may depend on polar $\phi\!\,$ and azimuth $\lambda\!\,$ direction of vector $r\!\,$ .

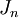The most widely used form of the gravitational potential function depends on $\phi\!\,$ (latitude) and potential coefficients, $J_n\!\,$ , called the zonal coefficients:

$E(r,\phi) = \frac{GM}{r} \left [1 - \sum_{n=2}^N J_{n} \left (\frac{R}{r} \right)^2 P_n (\sin \phi) \right ]$

[edit] Elastic potential energy

A catapult works due to elastic potential energy.

Main article: Elastic potential energy

Elastic potential energy is the potential energy of an elastic object (for example a bow or a catapult) that is deformed under tension or compression (often termed under the word stress by physicists). It arises as a consequence of a force that tries to restore the object to its original shape, which is most often the electromagnetic force between the atoms and molecules that constitute the object.

[edit] Calculation of elastic potential energy

In the case of a spring of natural length l and modulus of elasticity λ under an extension of x, elastic potential energy can be calculated using the formula:

$E = \frac{\lambda x^2}{2l}$

This formula is obtained from the integral of Hooke's Law:

$U_e = \int {k x}\, dx = \frac {1} {2} k x^2$

The equation is often used in calculations of positions of mechanical equilibrium.

In the general case, elastic energy is given by the Helmholtz potential per unit of volume f as a function of the strain tensor components ε_ij:

$f(\epsilon_{ij}) = \lambda \left ( \sum_{i=1}^{3} \epsilon_{ii}\right)^2+2\mu \sum_{i=1}^{3} \sum_{j=1}^{3} \epsilon_{ij}^2$

Where λ and μ are the Lamé elastical coefficients. The connection between stress tensor components and strain tensor components is:

$\sigma_{ij} = \left ( \frac{\partial f}{\partial \epsilon_{ij}} \right)_S$

For a material of Young's modulus, Y (same as modulus of elasticity λ), cross sectional area, A₀, initial length, l₀, which is stretched by a length, $Δ l$ :

$U_e = \int {\frac{Y A_0 \Delta l} {l_0}}\, dl = \frac {Y A_0 {\Delta l}^2} {2 l_0}$

where U_e is the elastic potential energy.

The elastic potential energy per unit volume is given by:

$\frac{U_e} {A_0 l_0} = \frac {Y {\Delta l}^2} {2 l_0^2} = \frac {1} {2} Y {\varepsilon}^2$

where $\varepsilon = \frac {\Delta l} {l_0}$ is the strain in the material.

[edit] Chemical potential energy

Chemical potential energy is a form of potential energy related to the structural arrangement of atoms or molecules. This arrangement may be the result of chemical bonds within a molecule or otherwise. Chemical energy of a chemical substance can be transformed to other forms of energy by a chemical reaction. For example, when a fuel is burned the chemical energy is converted to heat, same is the case with digestion of food metabolized in a biological organism. Green plants transform solar energy to chemical energy through the process known as photosynthesis, and electrical energy can be converted to chemical energy through electrochemical reactions.

The similar term chemical potential is used by chemists to indicate the potential of a substance to undergo a chemical reaction.

[edit] Electrical potential energy

Main article: electrical energy

An object can also have potential energy by virtue of its electric charge and several forces related to their presence. There are three main kinds of this kind of potential energy; electrostatic potential energy, electrodynamic potential energy (also sometimes called magnetic potential energy)and nuclear potential energy.

Strong electric field causing ionization (sparks) in gas.

[edit] Electrostatic potential energy

In case the electric charge of an object can be assumed to be at rest, it has potential energy due to its position relative to other charged objects.

The electrostatic potential energy is the energy of an electrically charged particle (at rest) in an electric field. It is defined as the work that must be done to move it from an infinite distance away to its present location, in the absence of any non-electrical forces on the object. This energy is non-zero if there is another electrically charged object nearby.

The simplest example is the case of two point-like objects A₁ and A₂ with electrical charges q₁ and q₂. The work W required to move A₁ from an infinite distance to a distance d away from A₂ is given by:

$W=k\frac {q_1q_2} d$

where k is Coulomb's constant, equal to $\frac 1 {4\pi\epsilon_0}$ .

This equation is obtained by integrating the Coulomb force between the limits of infinity and d.

A related quantity called electric potential is equal to electric potential energy of a unit charge.

[edit] Electrodynamic potential energy

In case a charged object or its constituent charged particles are not at rest, it generates a magnetic field giving rise to yet another form of potential energy, often termed as magnetic potential energy. This kind of potential energy is a result of the phenomenon magnetism, whereby an object that is magnetic has the potential to move other similar objects. Magnetic objects are said to have some magnetic moment. Magnetic fields and their effects are best studied under electrodynamics.

[edit] Nuclear potential energy

Nuclear potential energy, is the potential energy of the particles inside an atomic nucleus, some of which are indeed electrically charged. This kind of potential energy is different from the previous two kinds of electrical potential energies because in this case the charged particles are extremally close to each other. The nuclear particles are bound together not because of the coulombic force but due to strong nuclear force that binds nuclear particles more strongly and closely. Weak nuclear forces provide the potential energy for certain kinds of radioactive decay, such as beta decay.

Nuclear particles like protons and neutrons are not destroyed in fission and fusion processes, but collections of them have less mass than if they were individually free, and this mass difference is liberated as heat and radiation in nuclear reactions (the heat and radiation have the missing mass, but it often escapes from the system, where it is not measured). The energy from the Sun, also called solar energy, is an example of this form of energy conversion. In the Sun, the process of hydrogen fusion converts about 4 million metric tons of solar matter per second into light, which is radiated into space.

[edit] Thermal potential energy

Thermal energy of an object is simply a sum of average kinetic energy of random motion of particles constituting the object plus average potential energy of their displacement (from their equilibrium positions) as they oscillate/move around it. In case of ideal gas there is no potential energy due to interactions of particles, but kinetic energy may include rotational part too (for multiatomic gases) - if rotational levels are excited at given temperature T.

[edit] Rest mass energy

Albert Einstein was the first to calculate the amount of work needed to accelerate a body from rest to some finite speed using his definition of relativistic momentum. To his surprise, this work contained an extra term which did not vanish as the speed of accelerated body approached zero:

$E_0 = m c^2 \,$

This term (E₀) was therefore called rest mass energy, as m is the rest mass of the body (c is the speed of light in a vacuum). (The subscript zero is used here to distinguish this form of energy from the others that follow. In most other contexts, the equation is written with no subscript.)

So, the rest mass energy is the amount of energy inherent in the mass when it is at rest. If the mass changes, so must its rest mass energy which must be released or absorbed due to energy conservation law. Thus, this equation quantifies the equivalence of mass and energy.

Due to large numerical value of squared speed of light, even a small amount of mass is equivalent to a very large amount of energy, namely 90 petajoules per kilogram ≈ 21 megaton of TNT per kilogram.

[edit] Relation between potential energy and force

Potential energy is closely linked with forces. If the work done moving along a path which starts and ends in the same location is zero, then the force is said to be conservative and it is possible to define a numerical value of potential associated with every point in space. A force field can be re-obtained by taking the vector gradient of the potential field.

For example, gravity is a conservative force. The work done by a unit mass going from point A with $U = a$ to point B with $U = b$ by gravity is $(b - a)$ and the work done going back the other way is $(a - b)$ so that the total work done from

$U_{A \to B \to A} = (b - a) + (a - b) = 0 \,$

If we redefine the potential at A to be $a + c$ and the potential at B to be $b + c$ [where $c$ can be any number, positive or negative, but it must be the same number for all points] then the work done going from

$U_{A \to B} = (b + c) - (a + c) = b - a \,$

as before.

In practical terms, this means that you can set the zero of $U$ anywhere you like. You might set it to be zero at the surface of the Earth or you might find it more convenient to set it zero at infinity.

A thing to note about conservative forces is that the work done going from A to B does not depend on the route taken. If it did then it would be pointless to define a potential at each point in space. An example of a non-conservative force is friction. With friction, the route you take does affect the amount of work done, and it makes no sense at all to define a potential associated with friction.

All the examples above are actually force field stored energy (sometimes in disguise). For example in elastic potential energy, stretching an elastic material forces the atoms very slightly further apart. Equilibrium between electromagnetic forces and Pauli repulsion of electrons (they are fermions obeying Fermi statistics) is slightly violated resulting in small returning force. Scientists rarely talk about forces on an atomic scale. Often interactions are described in terms of energy rather than force. You can think of potential energy as being derived from force or you can think of force as being derived from potential energy (although last approach then requires independent from force definition of energy - which currently does not exist).

A conservative force can be expressed in the language of differential geometry as a closed form. Because Euclidean space is contractible, its de Rham cohomology vanishes, so every closed form is exact, i.e., is the gradient of a scalar field. This gives a mathematical justification of the fact that all conservative forces are gradients of a potential field.