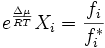Raoult's law
From Wikipedia, the free encyclopedia
Raoult's law states that
- The vapor pressure of an ideal solution is dependent on the vapor pressure of each chemical component and the mole fraction of the component present in the solution [1].
Once the components in the solution have reached chemical equilibrium, the total vapor pressure of the solution is:
and the individual vapor pressure for each component is
where
 is the vapor pressure of the pure component
is the vapor pressure of the pure component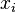 is the mole fraction of the component in solution
is the mole fraction of the component in solution
Consequently, as the number of components in a solution increases, the individual vapor pressures decrease, since the mole fraction of each component decreases with each additional component. If a pure solute which has zero vapor pressure (it will not evaporate) is dissolved in a solvent, the vapor pressure of the final solution will be lower than that of the pure solvent.
This law is strictly valid only under the assumption that the chemical interactions between the two liquids is equal to the bonding within the liquids: the conditions of an ideal solution. Therefore, comparing actual measured vapor pressures to predicted values from Raoult's law allows information about the relative strength of bonding between liquids to be obtained. If the measured value of vapor pressure is less than the predicted value, fewer molecules have left the solution than expected. This is put down to the strength of bonding between the liquids being greater than the bonding within the individual liquids, so fewer molecules have enough energy to leave the solution. Conversely, if the vapor pressure is greater than the predicted value more molecules have left the solution than expected, due to the bonding between the liquids being less strong than the bonding within each.
Contents
|
[edit] Deriving Raoult's Law (Raoult's Equation)
We define an ideal solution as a solution for which the chemical potential of component i is:
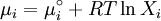 ,
,
where the reference state is the pure substance.
If the system is at equilibrium, then the chemical potential of the component i must be the same in the liquid solution and in the vapor above it. That is,
Assuming the liquid is an ideal solution, and using the formula for the chemical potential of a gas, gives:
 (1)
(1)
where
 is the fugacity of the vapor of i.
is the fugacity of the vapor of i.
If we study the component i in its pure state, we have:
where * indicates that we study a pure component.
But now, 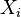 = 1, so
= 1, so
Subtracting both equations gives us
which can be written as
or
This equation is valid for the ideal solution.
Now, suppose the vapor of the solution behaves as an ideal gas. In this case, fugacity and pressure are identical, and we get
At equilibrium we have  = 0, and then
= 0, and then
Finally,
This last equality is what is known as Raoult’s Law.
[edit] Ideal mixing
An ideal solution can be said to follow Raoult's Law but it must be kept in mind that in the strict sense ideal solutions do not exist. The fact that the vapor is taken to be ideal is the least of our worries. Interactions between gas molecules are typically quite small especially if the vapor pressures are low. The interactions in a liquid however are very strong. For a solution to be ideal we must assume that it does not matter whether a molecule A has another A as neighbor or a B molecule. This is only approximately true if the two species are almost identical chemically. We can see that from considering the Gibbs free energy change of mixing:
This is always negative, so mixing is spontaneous. However the expression is -apart from a factor -T- equal to the entropy of mixing. This leaves no room at all for an enthalpy effect and implies that ΔHmix must be equal to zero and this can only be if the interactions U between the molecules are indifferent.
It can be shown using the Gibbs-Duhem equation that if Raoult's law holds over the entire concentration range x=0 to 1 in a binary solution that for the second component the same must hold.
If the deviations from ideality are not too strong, Raoult's law will still be valid in a narrow concentration range when approaching x=1 for the majority phase (the solvent). The solute will also show a linear limiting law but with a different coefficient. This law is known as Henry's law.
The presence of these limited linear regimes has been experimentally verified in a great number of cases.
[edit] Non-ideal mixing
Raoult's Law may be adapted to non-ideal solutions by incorporating two factors that will account for the interactions between molecules of different substances. The first factor is a correction for gas non-ideality, or deviations from the ideal-gas law. It is called the fugacity coefficient (φ). The second, the activity coefficient (γ), is a correction for interactions in the liquid phase between the different molecules.
This modified or extended Raoult's law is then written: