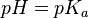Titration

From Wikipedia, the free encyclopedia

(Redirected from Titrant)

Jump to: navigation, search

In medicine, titration is the process of gradually adjusting the dose of a medication until the desired effect is achieved.

Titration setup: the titrant drops from the burette into the analyte solution in the flask. An indicator present then changes color permanently at the endpoint.

Titration is a common laboratory method of quantitative/chemical analysis which can be used to determine the concentration of a known reactant. Because volume measurements play a key role in titration, it is also known as volumetric analysis. A reagent, called the titrant, of known concentration (a standard solution) and volume is used to react with a solution of the analyte, whose concentration is not known in advance. Using a calibrated burette to add the titrant, it is possible to determine the exact amount that has been consumed when the endpoint is reached. The endpoint is the point at which the titration is complete, as determined by an indicator (see below). This is ideally the same volume as the equivalence point - the volume of added titrant at which the number of moles of titrant is equal to the number of moles of analyte, or some multiple thereof (as in polyprotic acids). In the classic strong acid-strong base titration the endpoint of a titration is when the pH of the reactant is just about equal to 7, and often when the solution permanently changes color due to an indicator. There are however many different types of titrations (see below).

Many methods can be used to indicate the endpoint of a reaction; titrations often use visual indicators (the reactant mixture changes colour). In simple acid-base titrations a pH indicator may be used, such as phenolphthalein, which becomes pink when a certain pH (about 8.2) is reached or exceeded. Another example is methyl orange, which is red in acids and yellow in alkali solutions.

Not every titration requires an indicator. In some cases, either the reactants or the products are strongly coloured and can serve as the "indicator". For example, an oxidation-reduction titration using potassium permanganate (pink/purple) as the titrant does not require an indicator. When the titrant is reduced, it turns colourless. After the equivalence point, there is excess titrant present. The equivalence point is identified from the first faint pink colour that persists in the solution being titrated.

Due to the logarithmic nature of the pH curve, the transitions are generally extremely sharp, and thus a single drop of titrant just before the endpoint can change the pH significantly — leading to an immediate colour change in the indicator. That said, there is a slight difference between the change in indicator color and the actual equivalence point of the titration. This error is referred to as an indicator error, and it is indeterminate.

1 History and etymology
2 Preparing a sample for titration
3 Procedure
4 Titration curves
5 Types of titrations
6 Measuring the endpoint of a titration
- 6.1 Other terms
7 Particular uses
8 References
9 External links

[edit] History and etymology

The word "titration" comes from the Latin word "titalus", meaning inscription or title. The French word, titre, also from this origin, means rank. Titration, by definition, is the determination of rank or concentration of a solution with respect to water with a pH of 7 (which is the pH of pure water), so it corresponds.

The origins of volumetric analysis are in late 18th century French chemistry. Francois Antoine Henri Descroizilles developed the first burette (which looked more like a graduated cylinder) in 1791. Joseph Louis Gay-Lussac developed an improved version of the burette that included a side arm, and coined the terms "pipette" and "burette" in a 1824 paper on the standardization of indigo solutions. A major breakthrough in the methodology and popularization of volumetric analysis was due to Karl Friedrich Mohr, who redesigned the burette by placing a clamp and a tip at the bottom, and wrote the first textbook on the topic, Lehrbuch der chemisch-analytischen Titrirmethode (Textbook of analytical-chemical titration methods), published in 1855.^[1]

[edit] Preparing a sample for titration

In a titration, both titrant and analyte are required to be aqueous, or in a solution form. If the sample isn't a liquid or solution, the samples must be dissolved. If the analyte is very concentrated in the sample, it might be useful to dilute the sample.

Although the vast majority of titrations are carried out in aqueous solution, other solvents such as glacial acetic acid or ethanol (in petrochemistry) are used for special purposes.

A measured amount of the sample can be given in the flask and then be dissolved or diluted. The mathematical result of the titration can be calculated directly with the measured amount. Sometimes the sample is dissolved or diluted beforehand and a measured amount of the solution is used for titration. In this case the dissolving or diluting must be done accurately with a known coefficient because the mathematical result of the titration must be multiplied with this factor.

Many titrations require buffering to maintain a certain pH for the reaction. Therefore, buffer solutions are added to the reactant solution in the flask.

Some titrations require "masking" of a certain ion. This can be necessary when two reactants in the sample would react with the titrant and only one of them must be analysed, or when the reaction would be disturbed or inhibited by this ion. In this case another solution is added to the sample which "masks" the unwanted ion (for instance by a weak binding with it or even forming a solid insoluble substance with it).

Some redox reactions may require heating the solution with the sample and titration while the solution is still hot (to increase the reaction rate).

[edit] Procedure

A typical titration begins with a beaker or Erlenmeyer flask containing a precisely known volume of the reactant and a small amount of indicator, placed underneath a burette containing the reagent. By controlling the amount of reagent that is added to the reactant, it is possible to detect the point at which the indicator changes colour. As long as the indicator has been chosen correctly, this should also be the point where the reactant and reagent neutralise each other, and by reading the scale on the burette the volume of reagent can be measured.

As the concentration of the reagent is known, the number of moles of reagent can be calculated (since $c o n c e n t r a t i o n = m o l e s / v o l u m e$ ). Then, from the chemical equation involving the two substances, the number of moles present in the reactant can be found. Finally, by dividing the number of moles of reactant by its volume, the concentration is calculated.

[edit] Titration curves

It has been suggested that some content from this article be split into a separate article entitled Titration curve. (Discuss)

A typical titration curve of a diprotic acid, oxalic acid, titrated with a strong base, sodium hydroxide. Each of the two equivalence points are visible

Titrations are often recorded on titration curves, whose compositions are generally identical: the independent variable is the volume of the titrant, while the dependent variable is the pH of the solution (which changes depending on the composition of the two solutions). The equivalence point is a significant point on the graph (the point at which all of the starting solution, usually an acid, has been neutralized by the titrant, usually a base). It can be calculated precisely by finding the second derivative of the titration curve and computing the points of inflection (where the graph changes concavity); however, in most cases, simple visual inspection of the curve will suffice (in the curve given to the right, both equivalence points are visible, after roughly 15 and 30 mL of NaOH solution has been titrated into the oxalic acid solution.) To calculate the pKa values, one must find the volume at the half-equivalence point, that is where half the amount of titrant has been added to form the next compound (here, sodium hydrogen oxalate, then disodium oxalate). Halfway between each equivalence point, at 7.5 mL and 22.5 mL, the pH observed was about 1.5 and 4, giving the pKa values.

In monoprotic acids, the point halfway between the beginning of the curve (before any titrant has been added) and the equivalence point is significant: at that point, the concentrations of the two solutions (the titrant and the original solution) are equal. Therefore, the Henderson-Hasselbalch equation can be solved in this manner:

$pH = pK_a + \log \left( \frac{[\mbox{base}]}{[\mbox{acid}]} \right)$

$pH = pK_a + \log(1)\,$

$pH = pK_a \,$

Therefore, one can easily find the acid dissociation constant of the monoprotic acid by finding the pH of the point halfway between the beginning of the curve and the equivalence point, and solving the simplified equation. In the case of the sample curve, the K_a would be approximately 1.78×10^-5 from visual inspection (the actual K_a2 is 1.7×10^-5)

For polyprotic acids, calculating the acid dissociation constants is only marginally more difficult: the first acid dissociation constant can be calculated the same way as it would be calculated in a monoprotic acid. The second acid dissociation constant, however, is the point halfway between the first equivalence point and the second equivalence point (and so on for acids that release more than two protons, such as phosphoric acid).

[edit] Types of titrations

Titrations can be classified by the type of reaction. Different types of titration reaction include:

Acid-base titration is based on the neutralization reaction between the analyte and an acidic or basic titrant. These most commonly use a pH indicator, a pH meter, or a conductance meter to determine the endpoint.
A Redox titration is based on an oxidation-reduction reaction between the analyte and titrant. These most commonly use a potentiometer or a redox indicator to determine the endpoint. Frequently either the reactants or the titrant have a colour intense enough that an additional indicator is not needed.
A Complexometric titration is based on the formation of a complex between the analyte and the titrant. The chelating agent EDTA is very commonly used to titrate metal ions in solution. These titrations generally require specialized indicators that form weaker complexes with the analyte. A common example is Eriochrome Black T for the titration of calcium and magnesium ions.
A form of titration can also be used to determine the concentration of a virus or bacterium. The original sample is diluted (in some fixed ratio, such as 1:1, 1:2, 1:4, 1:8, etc.) until the last dilution does not give a positive test for the presence of the virus. This value, the titre, may be based on TCID50, EID50, ELD50, LD₅₀ or pfu. This procedure is more commonly known as an assay.

[edit] Measuring the endpoint of a titration

Main article: Endpoint (chemistry)

Different methods to determine the endpoint include:

pH indicator: This is a substance that changes colour in response to a chemical change. An acid-base indicator (e.g., phenolphthalein) changes colour depending on the pH. Redox indicators are also frequently used. A drop of indicator solution is added to the titration at the start; when the colour changes the endpoint has been reached.
A potentiometer can also be used. This is an instrument which measures the electrode potential of the solution. These are used for titrations based on a redox reaction; the potential of the working electrode will suddenly change as the endpoint is reached.
pH meter: This is a potentiometer which uses an electrode whose potential depends on the amount of H+ ion present in the solution. (This is an example of an ion selective electrode. This allows the pH of the solution to be measured throughout the titration. At the end point there will be a sudden change in the measured pH. It can be more accurate than the indicator method, and is very easily automated.
Conductance: The conductivity of a solution depends on the ions that are present in it. During many titrations, the conductivity changes significantly. (For instance, during an acid-base titration, the H+ and OH- ions react to form neutral H₂O. This changes the conductivity of the solution.) The total conductance of the solution depends also on the other ions present in the solution (such as counter ions). Not all ions contribute equally to the conductivity; this also depends on the mobility of each ion and on the total concentration of ions (ionic strength). Thus, predicting the change in conductivity is harder than measuring it.
Colour change: In some reactions, the solution changes colour without any added indicator. This is often seen in redox titrations, for instance, when the different oxidation states of the product and reactant produce different colours.
Precipitation: If the reaction forms a solid, then a precipitate will form during the titration. A classic example is the reaction between Ag+ and Cl- to form the very insoluble salt AgCl. Surprisingly, this usually makes it difficult to determine the endpoint precisely. As a result, precipitation titrations often have to be done as "back" titrations (see below).
An isothermal titration calorimeter uses the heat produced or consumed by the reaction to determine the endpoint. This is important in biochemical titrations, such as the determination of how substrates bind to enzymes.
Thermometric titrimetry is an extraordinarily versatile technique. This is differentiated from calorimetric titrimetry by the fact that the heat of the reaction (as indicated by temperature rise or fall) is not used to determine the amount of analyte in the sample solution. Instead, the endpoint is determined by the rate of temperature change.
Spectroscopy can be used to measure the absorption of light by the solution during the titration, if the spectrum of the reactant, titrant or product is known. The relative amounts of the product and reactant can be used to determine the endpoint.
Amperometry can be used as a detection technique (amperometric titration). The current due to the oxidation or reduction of either the reactants or products at a working electrode will depend on the concentration of that species in solution. The endpoint can then be detected as a change in the current. This method is most useful when the excess titrant can be reduced, as in the titration of halides with Ag+. (This is handy also in that it ignores precipitates.)

[edit] Other terms

The term back titration is used when a titration is done "backwards": instead of titrating the original analyte, one adds a known excess of a standard reagent to the solution, then titrates the excess. A back titration is useful if the end point of the reverse titration is easier to identify than the end point of the normal titration. They are also useful if the reaction between the analyte and the titrant is very slow.

[edit] Particular uses

As applied to biodiesel, titration is the act of determining the acidity of a sample of WVO by the dropwise addition of a known base to the sample while testing with pH paper for the desired neutral pH=7 reading. By knowing how much base neutralizes an amount of WVO, we discern how much base to add to the entire batch.
Titrations in the petrochemical or food industry to define oils, fats or biodiesel and similar substances. An example procedure for all three can be found here: [1].
- Acid number: an acid-base titration with colour indicator is used to determine the free fatty acid content. See also: pH of fatty acids.
- Iodine number: a redox titration with colour indication which indicates the amount of unsaturated fatty acids.
- Saponification value: an acid-base back titration with colour indicator or potentiometric to get a hint about the average chain length of fatty acids in a fat.